| |
Geometry Group
Members
Projects
Lehre
Seminare
Archive
|
|
|
- Instructors:
| Lectures |
Dr. Charles Gunn |
Di |
10-12 |
MA 212 |
| Do |
10-12 |
MA 212 |
| Tutorial |
Dr. Charles Gunn |
Di,Do |
12-14 |
MA 313 |
- Current:
- [05.09.13] Most communications regarding the course will take place using this blog originally created for last year's course. You can look around there to get a rough idea of the structure of the course, although due to the new teacher this year there will be differences in emphasis.
- [05.09.13] The first meeting of the tutorial will be Tuesday Sept 15 at 14:00 in MA 313. Further schedule for the tutorial will be decided at that meeting based on the schedules of the participants.
- [20.09.13] I've posted a first post on the course blog with some opening words on the course. Due to spam problems, this blog is password protected.
- [21.10.13]The lecture on Thursday, 31.10.2013 will be held in MA 848 instead of MA 212.
- Contents:
- The course will introduce students to mathematical visualization. Various mathematical themes will be developed that have a particular affinity to visualization, including euclidean and non-euclidean geometry, symmetry groups, and geometric algebra. Students will be introduced to the "handwork" of mathematical visualization by designing and creating their own semester projects (typically in groups of 2) based on a theme of their own choosing. Possible forms for this project include interactive applications, animations, and 3D prints. See last year's website for a gallery of last year's student projects.
- Assignment of a grade for the course will be based on the semester project considered as a "Prüfungsrelevante Studiumsleistung". Students who choose to do so may also obtain a seminar certificate by presenting a lecture on the project to the Seminar of the AG Geometrie.
- Projects:
Here is the schedule for the student project presentations in April. The presentations should be 35-40 minutes long with 10-5 minutes for questions and discussions, and 5 minute pause.
Monday April 7
- 10 am Alexander Rettkowski, "Von der Schönheit des mathematischen Chaos" ["On the Beauty of Mathematical Chaos"]
- 10:50 Theresa Thunig and Nadja Goerigk, "Unfolding Textured Polyhedra"
- 11:40 Juliane Pawlitzki and Viktoria Langer, "Sphere-handling Interface of Escher-like Drawing"
Tuesday April 8
- 10 pm Christof Seidel and Robert Volkmann, "Unwrapping 3D tori to the plane"
- 10:50 Mats Olthoff and Michael Kreuz, "Colouring objects and symmetry group actions"
- 11:40 Peter Kleisinger and Gerald Bartz, "A Euclidean Tetrahedral Kaleidoscope"
- 14:00 Lisa Rieder and Rhoslyn Coles, "Visualizing Complex Functions"
- 14:50 Richard Luetzke and Pedro de las Casas, "Painting on Wallpaper Orbifolds"
- 15:40 Charles Gunn, "The current state of the conformal movie" (10 minutes)
Wednesday April 9
- 10 pm Martin Swiontek Brzezinski and Sophia Lee, "Escher's Wallpapers"
- 10:50 Nick Bremer, "More on circle packings on orbifolds" (10 minutes)
- 11:40 Luis Vera, "The Whisper Gallery: Sonification Experiments with Wallpaper Groups"
- 14:00 Michael Joos and Ingo Gühring, "Isohedral Tilings of the Plane"
- 14:50 Fabian Heil and Torben Meyer zur Natrup, "Cellular Automata on Euclidean Orbifolds"
- 15:40 Hardy Gurack and Andre Schäller, "Realtime Stereograms in jReality"
Here is a listing of the student projects. - Clicking on the image on the left side activates the Webstart application associated to the project.
- To obtain on-line documentation, click on the main graphics window and type 'h'.
- If you have problems getting the Webstart applications to run on your computer, here is a trouble-shooting page.
-
 |
Packing circles on a cylinder
In this project from Michael Gubik and Nick Bremer, randomly generated circles are packed onto a cylinder. The different lengths of the cylinder can minimized such that all circles still fit onto it. The project illustrates the optimization process by showing various solutions (in 2D as well as 3D). The user can generate different circle sets, select different optimization goals, safe and load previous fits and ultimately create virtual art objects. The inner workings are based in large parts on "Greedy Algorithms for Packing Unequal Circles into a Rectangular Container" by WenQi HUANG, Yu LI, Hakim AKEB and ChuMin LI.
|
 |
The shadow problem in 3-space
(slides)
This project from Tatiana Gonzalez Grandon allows the user to play around with different surfaces (torus, ellipsoid, elliptic paraboloid, hyperbolic paraboloid, helicoid, Mobius strip, torus knots, etc) to learn about the concept of shadows and shadow boundaries. The user can select the light vector and some parameters for each surface and instantly see what the shadow and its boundary look like, also included are parameters to control the resolution and the tolerance for the boundary to create a better representation.
|
 |
Seltsame Attraktoren mit jReality
(slides)
In this project, Alexander Rettkowski visualizes a lot of different strange attractors. He provides the possibility
to change different parameters and test for chaotic behavior.
The user creates an attractor based on one of the different presets and changes coefficients. Then he can calculate
the fractal dimension and the first Lyapunov exponent of what he has done.
|
 |
Unfolding Textured Polyhedra
Using the program from Theresa Thunig and Nadja Goerigk, one can easily produce printing templates for
textured polyhedra. Just enter your own spherical panorama, choose the polyhedron and print the unfolding. By cutting
and gluing you will get your impression back as a real 3D object!
|
 |
Sphere-Handling Interface of Escher-Like Drawings
This project from Viktoria Langer and Juliane Pawlitzki is an interactive tool for creating mathematical art based on Escher-tilings on spheres. The user can choose from the symmetry groups 233, 245 and 235, change the boundary of a given fundamental domain arbitrarily and interpolate the resulting curve with b-splines of order 3. Enjoy.
|
 |
Unwrapping 3D tori to the plane
This project from Christoph Seidel and Robert Volkmann creates an animation tool to visualize the deformation of a 3D torus to a polygon.
The user can control four different deformation types by five algorithms. It is possible to resample the whole animation.
|
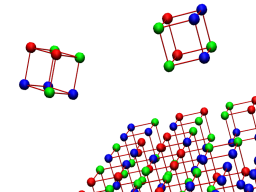 |
Colouring objects and symmetry group actions
(slides)
This project written by Mats Olthoff and Michael Kreutz creates a playful environment for visualizing simple examples for Polya Theorie, i.e. equivalence
of coloured mathematical objects under certain symmetries.
The user chooses a mathematical object and specifies what to colour before being able to explore equivalent objects and
being convinced that they can be transformed into one another.
|
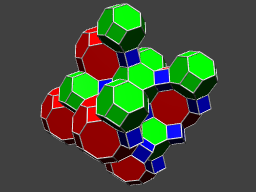 |
Tesselating Three Dimensional Space with a Euclidean Kaleidoscope
(slides)
This project from Gerald Bartz and Peter Kleisinger creates an environment for learning about the space kaleidoscope group [4,3,4]. The program allows the user to explore different regular space tesselations which come from applying the space kaleidoscope group to different geometries. The position of a special point inside the fundamental domain can be changed which creates also non-regular tesselations The user can also fly around in the scene.
|
 |
Visualizing Complex Functions
This project, from Rhoslyn Coles and Lisa Rieder, provides a colorful representation of complex functions. Complex functions cannot be drawn using traditional graph methods and hence can be difficult to imagine. Here the method of Domain Coloring is used to encode the value of complex functions at a point in the domain in terms of a color hue and the color quality, i.e. saturation and brightness.
The domain coloring pictures aim to help mathematics students understand complex functions both in the plane and on the Riemann Sphere.
Several aspects of complex functions, such as the poles and zeros of the function can be clearly displayed in the domain coloring graphs, as well as the behaviour of functions in the neighbourhoods of such points.
The software tool is a good introduction to domain coloring graphs and provides students with the opportunity to get a feel for complex functions.
|
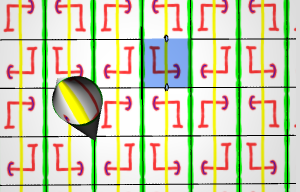 |
Painting on Wallpaper Orbifolds
The goal of this project by Richard Luetzke and Pedro Maristany was to create a visualization of the
wallpaper symmetry groups. To better visualize
them, we show the tessellation of the group as well as the respective
orbifold. The user can draw on either figure and observe how the drawing is multiplied on the tessellation and in what way the boundaries of the
fundamental domain, a single tile of the tessellation, are mapped onto each other on the orbifold.
|
 |
Escher's Wallpapers
(slides)
The program Escher Painter designed by Sophia Lee and Martin Swiontek Brzezinski has its main purpose in supporting the creation of an Escher-style tessellation, i.e. to create a repeat pattern with a single tile, which can be painted.
The type of pattern can be chosen out of 17 so-called wallpaper groups, that use translation, rotation and other means for creating a pattern.
|
 |
The Whisper Gallery
(slides)
(Luis Vera) The main idea of this project is provide the user a 'sensorial embedding' within the wallpaper groups via the euclidean orbifolds.
For this purpose, we create a 3D graphical environment that extends the underlying structure of these bidimensional spaces
and also resort to the concept of 'sonification', in order to model the propagation of the sound within each orbifold;
this allows the user to experience the unintuitive sequence of reflections and identifications that his own voice would suffer.
|
 |
Isohedral Tilings in the Plane
This Project from Ingo Guehring and Michael Joos creates an environment to draw different types of isohedral tilings.
The user can choose the type of tiling, specify parameters for the tiling vertices and manipulate the edge shapes
arbitrarily.
|
 |
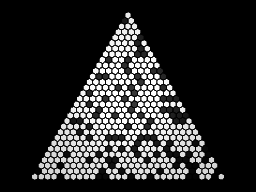
Non-Euclidean Tetrahedral Kaleidoscopes
This project from Alina M. Hinzmann and Lisa Dörr was designed to experience different spherical and hyperbolic kaleidoscopes and to see how space can be tesselated with their use. Every kaleidoscope is a special tetrahedron with its faceplanes working as mirrors. It will be the basis for many different uniform polychora and honeycombs. Besides selecting a particular kaleidoscope the user can choose between two different modes for generating a geometry. This geometry sits inside the kaleidoscope and will thus be mirrored and might fill space.
|
 |
Cellular Automata on Euclidean Orbifolds
(slides)
The project "Cellular Automata on Euclidean Orbifolds" is based on Conway's Game of Life a 0-player game and probably the most known example for a Cellular Automaton. It connects two fields (Cellular Automata and Euclidean Orbifolds) that don't seem to have any connection. With this program you can discover Conway's Game of Life (and other cellular automata) and how they behave on different underlying regions. Created by Fabian Heil and Torben Meyer zu Natrup
|
 |
Realtime Stereograms in jReality
(slides)
June 6, 2014: This project is currently not working. Please check back soon.
This project from Andre Schaller and Hardy Gurack enables the user to view every jReality scene as a stereogram, just like in famous the "magic eye" books.
Stereograms are created by distortion of repetitive patterns and can be seen by focusing your eyes in a special way.
Our project provides a jReality plugin which is easy implementable.
You can create your own stereograms with your scene, which will be disguised by choosable and moveable backgrounds.
Warning: this application only works on computers with OpenGL 4.0 driver support.
|
 |
Spherical symmetry groups
This project from Wingthor and Loki provides an introduction to the spherical symmetry groups based on the platonic solids 233, 234 and 235.
|
- Technology
-
We will use the Java libraries jReality and jtem (both developed here at TU Berlin) for technical realization of the projects. The resulting applications will then also run in the PORTAL . There is also a chance to use the 3D printing facilities at the 3D Lab in the Math building.
- Policies:
- Due dates for homework assignments are sharp: no extensions will be given without a medical excuse.
-
- Contact:
| Office hours |
Gunn> |
TBA |
|
MA 884 |
|



