Virtual Math Labs: Curves & Surfaces

Planar Curve Explorer

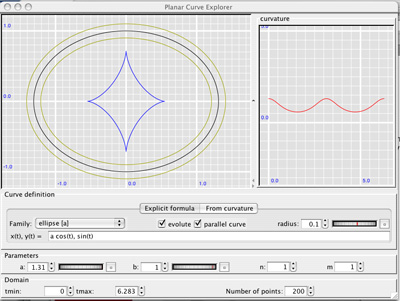This application allows the user to explore planar curves:

• Specification by
  • parametric formula (x(t), y(t))
  • from curvature function k(t)
• Optional display of
  • parallel curve
  • evolute curve
• Display of curvature graph

Space Curve Explorer

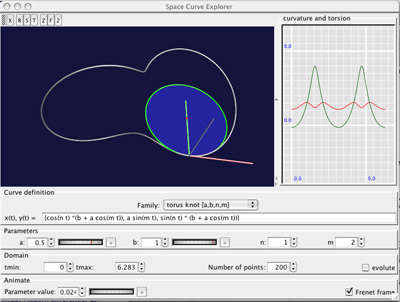This application allows the user to explore space curves:

• Specification by parametric formula (x(t), y(t), z(t))
• Menu of built-in examples.
• Optional display of evolute curve.
• Display of curvature and torsion graphs
• Animated display of Frenet frame and osculating circle.

Surface Explorer

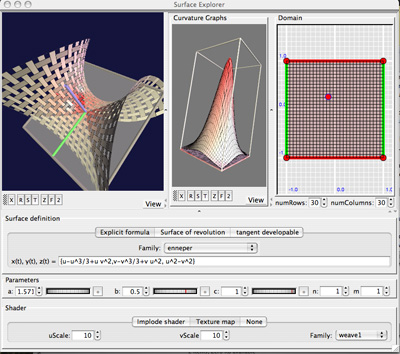This application allows the user to explore surface patches in R3:

• Specification by parametric formula (x(u,v), y(u,v), z(u,v))
• A menu containing many built-in examples.
• Interactive specification of definition rectangle.
• Display of Gaussian curvature and mean curvature graphs
• Draggable tangent plane and optional second order approximation.
• Sophisticated interactive 3D viewer with customized shading options

Visualization in Geometric Knot Theory

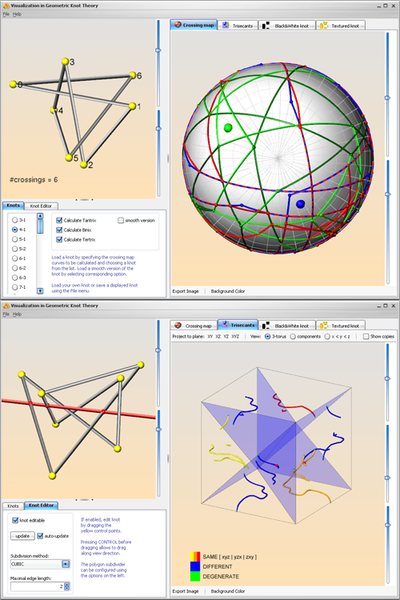A jReality application realizing different interactive visualizations in geometric knot theory.

• load, edit and save knots
• explore the crossing map of a given knot
• analyze the set of trisecants of a given knot and find quadrisecants
• create images of textured knots

Most program options are available via the context menu of corresponding components and their toolbars and sliders. Rotate displayed objects using the left mouse button. For further information see the application's Help menu.

This lab was implemented by Martin Sommer as part of his Diploma Thesis "Visualization in Geometric Knot Theory - Understanding the mathematical structure of trisecants" using the jReality library.

Tractrix

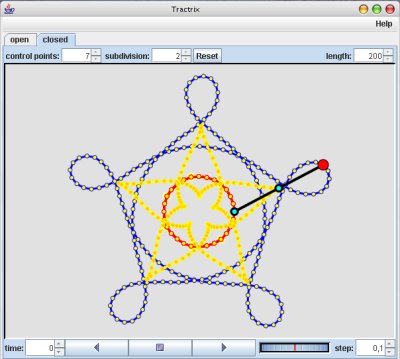This application allows to explore polygonal tractrix curves.

For more information see the online help of the application.

Geodesics on Parametric Surfaces

Geodesics on Spheres of Revolution

Geodesics on Tori of Revolution

Implicit Surfaces

Parametric Surface Viewer

Frenet Frames

Closed Elastic Curves

Rectifiable Curves

Delaunay Triangulation

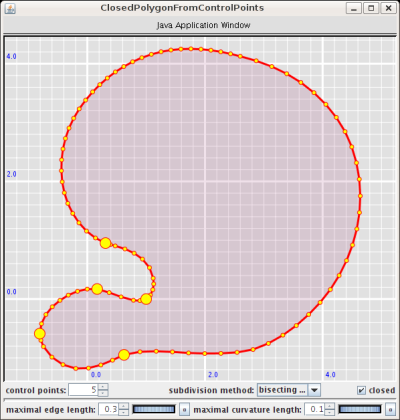
This lab generates the triangulation of any number of points. You may change the number of points. When you drag the points around the triangulation will be adjusted interactively.

Press 'e' to encompass and <CTRL>-<Left Mouse Button>.

Lab author: Markus Schmies

Subdivision

K-surfaces with a planar strip

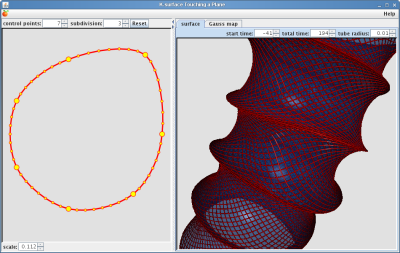A K-Surface is a surface of constant negative Gaussian curvature. The planar strip may be edited on the left. On the right you may investigate the surface and its Gauss map. The Gauss map may be seen as the evolution of massive balls on the sphere connected by rubber bands. There is a small mpeg (2MiB) video or animated gif (11MiB). More ...

For the theoretical background consult Designing Cylinders with Constant Negative Curvature.

Ulrich Pinkall

K-surfaces with a cone point

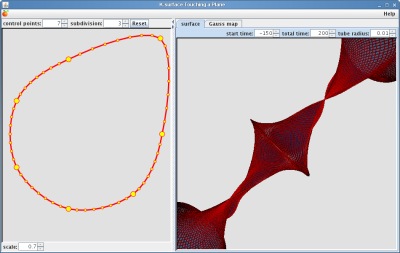A K-Surface is a surface of constant negative Gaussian curvature. The initial Gauss map may be edited on the left. On the right hand side you may investigate the surface and its Gauss map. The Gauss map may be seen as the evolution of massive balls on the sphere connected by rubber bands. More ...

For the theoretical background consult Designing Cylinders with Constant Negative Curvature.

Ulrich Pinkall

Surfaces of Constant Gaussian Curvature

In this lab you may investigate surfaces of constant negative Gaussian curvature (K-surfaces). Double click on the surface allows you to change the curvature and the length of the surface. The initial curve may be changed (at the bottom when the lab comes up). Just drag the yellow points of the initial curve. Double click on the initial curve to add more control points and change the interpolation parameters. Double click on the initial curve to open a panel that allows to change the number of control points and subdivision parameters. More ... .

The labs front end uses ViewerVR from our jReality project. You may wish to have a look at the ViewerVR User Manual.

For the theoretical background consult Designing Cylinders with Constant Negative Curvature.

Ulrich Pinkall