Homotopy Methods for Dynamic Flows

 

Funding

Math+ project IN-6

Project head
Max Klimm

Project member
Philipp Warode

Project duration
01.01.2022 - 31.12.2022

Private motorized transport has an enormous impact on life in modern cities. Not only are large parts of the urban infrastructure planned around road traffic and optimized for it. Road traffic also accounts for a not insignificant share of noise, air and environmental pollution as well as the emission of climate-damaging gases.

Therefore, it is essential for modern urban planning to understand inner-city individual traffic and the underlying dynamics and to use the resulting insights to improve the traffic situation.

We look at road traffic from a game theoretic perspective: A set of agents (the drivers) with individual objectives (moving from A to B in a road network) can choose from a set of possible strategies (different routes). When following a strategies, the agents influence each others's travel time by inducing congestion on the roads they use. Assuming that the agents act rational and selfish, everyone strive to choose a fastest route possible. Since a large number of players repeats this game over and over, from a macroscopic view the overall situation converges to an equilibrium state where no agent can improve their route individually.

Since we are mainly interested in a macroscopic view of the situation, we consider models that treat the road traffic as a continuous stream of infinitesimally small particles rather than an interaction of individual agents. The underlying mathematical object to model this is a flow. Equilibrium flow models like the widely used Wardrop equilibrium model have been used for a long time to model road traffic.

The disadvantage of the Wardrop equilibrium and related models is that it only considers static flows. In such models, flow is thought to be travelling with a constant, static rate through the network. While this allows for a rather good approximation of traffic flows in relatively constant situation on the larger scale, such as the traffic flow in rush hour conditions, static flow models lack the ability to accurately model the underlying dynamics of traffic.

In order to model more the more complex dynamics, we consider Flows over time first introduced by Ford and Fulkerson. Koch and Skutella introduced the following model for Nash flows over time, where infinitesimally small particles move through a network consisting of edges. For every edge, there is a fixed time that is needed to traverse the respective edge as well as a capacity. If the capacity is exceeded, queues build on the edges, slowing the particles down. This is why this model is also referred to as the dynamic queuing model. A Nash flow in this setting is a flow where every particle travels only on shortest paths.

Instance: A flow over time network

• Graph $G = (V,E)$ with vertices $V$ and edges $E$
  The road network where the roads are represented by the edges and intersections are represented by the vertices.
• Edge travel times $\tau_e \geq 0, e \in E$
  The time that a particle/driver needs to traverse the edge $e \in E$ without any congestion.
• Edge capacities $\nu_e > 0, e \in E$
  The amount of particles/drivers that can traverse an edge within one time unit. If the capacities are exceeded, queues start to build up on the edges.
• Inflowrate at some source vertex $s \in V$ given as a function $u : \mathbb{R}_{\geq 0} \to \mathbb{R}_{\geq 0}$, a terminal vertex $t$
  The inflow rate of traffic that enters the network at the specific vertex $s$ depending on the time and the target target vertex $t$.

Solution: A Nash flow over time

• Inflow functions $f^+_e : \mathbb{R}_{\geq 0} \to \mathbb{R}_{\geq 0}$ and outflow functions $f^-_e : \mathbb{R}_{\geq 0} \to \mathbb{R}_{\geq 0}$ for all vertices that satisfy the following conditions
  Functions that specify the amount of flow entering and leaving at every given point in time.
• $\displaystyle \sum_{e \in \delta^+(v)} f^+_e (\theta) - \sum_{e \in \delta^-(v)} f^-_e (\theta) = \begin{cases} u(\theta) & \text{if } v = s, \\ 0 & \text{if } v \neq s, t \end{cases}$
  Flow conservation: In- and outflow sum to zero (if $v \neq s, t$) or to the inflow rate (at $v = s$).
• For almost all points in time $\theta$, for every edge $e = (v,w) \in E$ with $f^+(\theta) > 0$, we have \[ l_w( \theta ) = l_v (\theta) + \frac{z_e(l_v(\theta))}{\nu_e} + \tau_e \] where
  • $l_v (\theta)$ is the earliest point in time, where a particle entering the network at time $\theta$ can reach vertex~$v$
  • $z_e(\theta)$ is the amount of flow waiting in a queue on edge $e$ at time $\theta$.
  Equilibrium conditions: Every particle moves only on edges such that the particle arrives at the next vertex as early as possible. This implies no particle has an incentive to deviate to another path in this configuration.

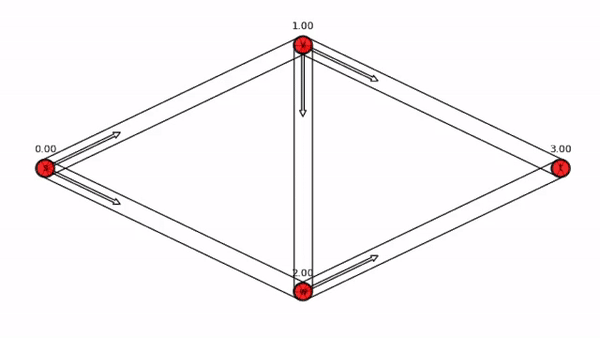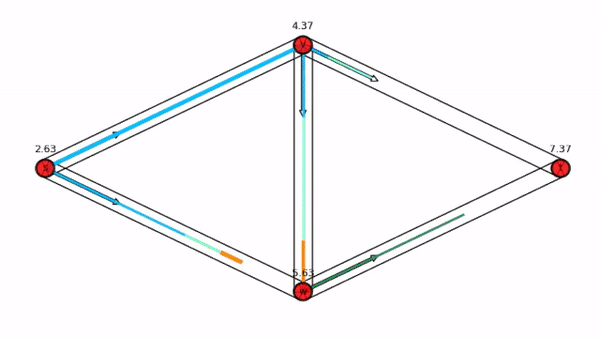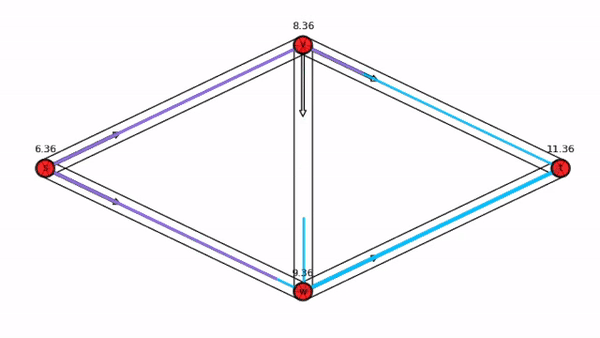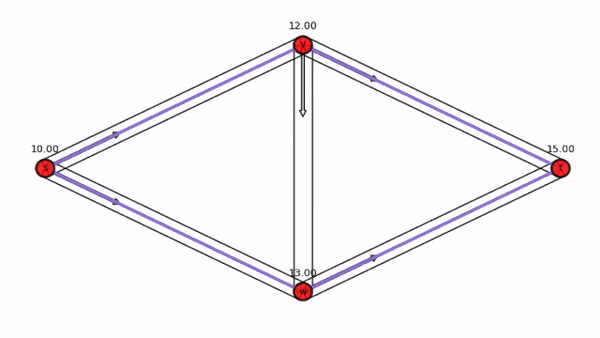A Nash flow over time.

Animation generated with Nash Flow Computation Tool

Although Nash flows over time have been researched for many years now, there are still many open questions regarding the model.

Open questions

• Does the equilibrium flow consist of finitely many phases?
  It is known that a Nash flow over time consists of consecutive phases in which the in- and outflow rates are constant. However, it is not yet knwon, whether the number of this phases is finite.
• How there an efficient way to compute thin flows? If not, what is the complexity of computing a thin flow?
  The computation of Nash flows over time relies on the computation of the derivatives of the flows that are also called thin flows. There is no known, efficient algorithm to compute these flows.

Our approach

In previous work we developed homotopy methods to compute parametrized Nash equilibrium flows in the static Wardrop equilibrium model. The solution flows of in these models can be expressed as solutions to differential equations on piecewise linear vector fields. Since the same holds true for the dynamic queuing model and we were able to develop efficient computation schemes for the static case, we hope to extend our techniques also to the dynamic flow case.

References