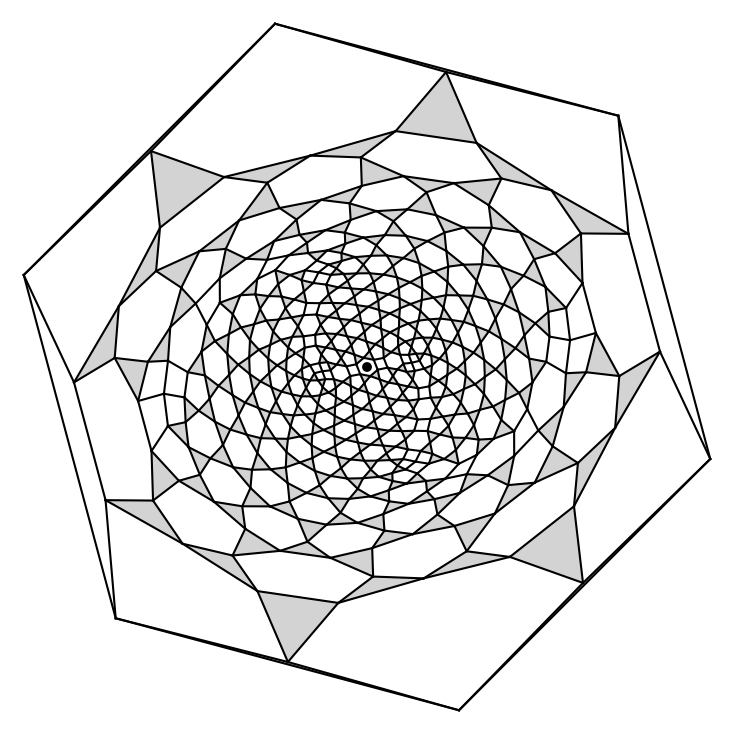
> triangles
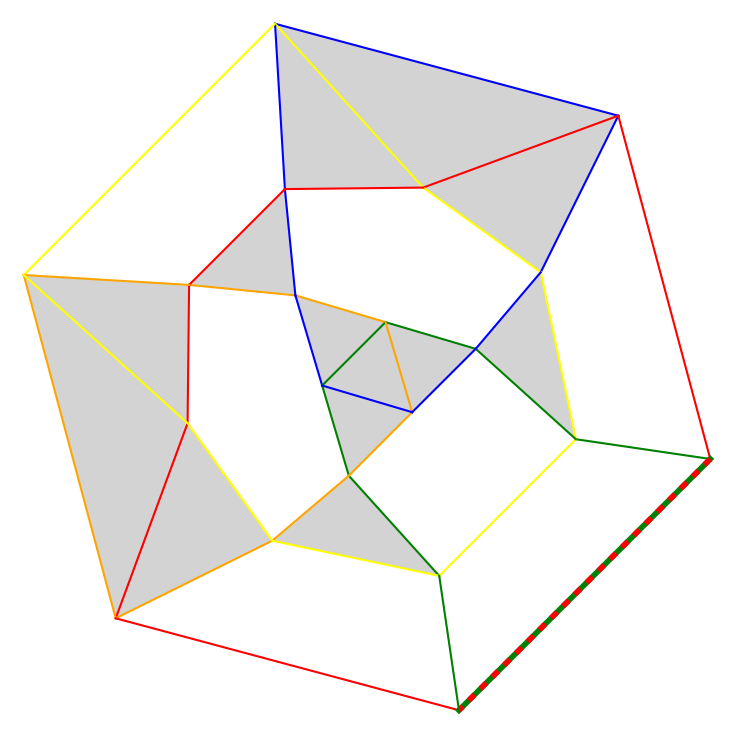
Go back... This page provides- digon-free arrangements of up to $n=14$ pseudocircles which obtain the minimum number of triangles,
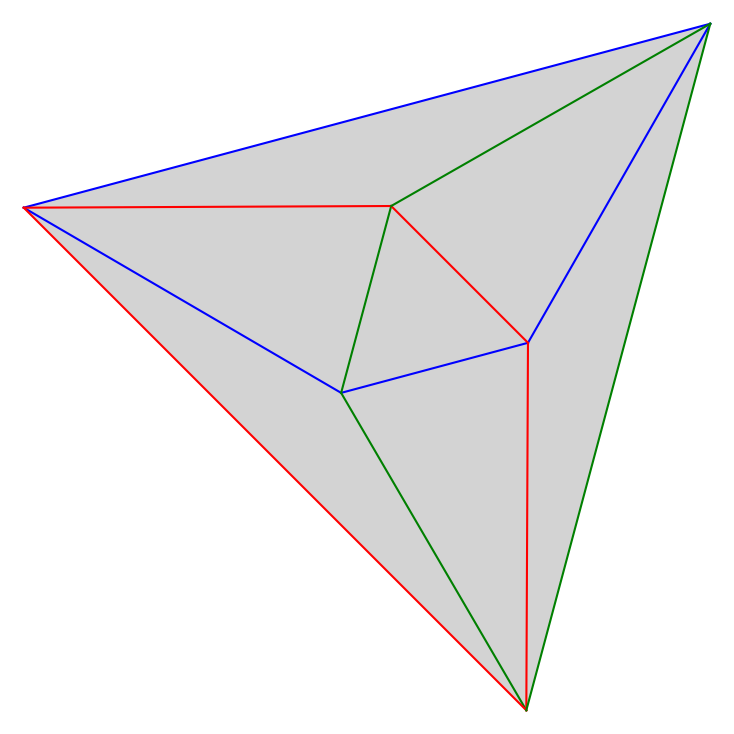
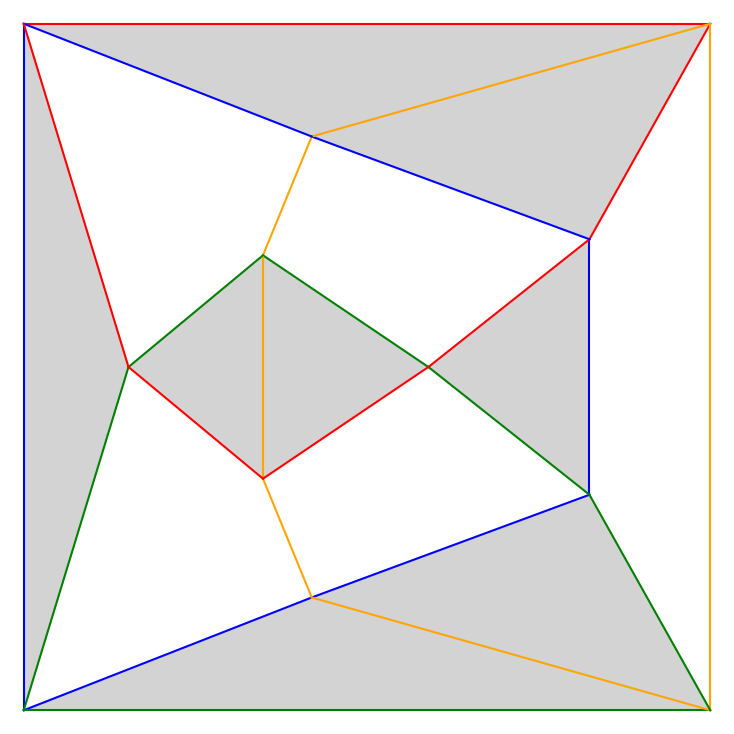
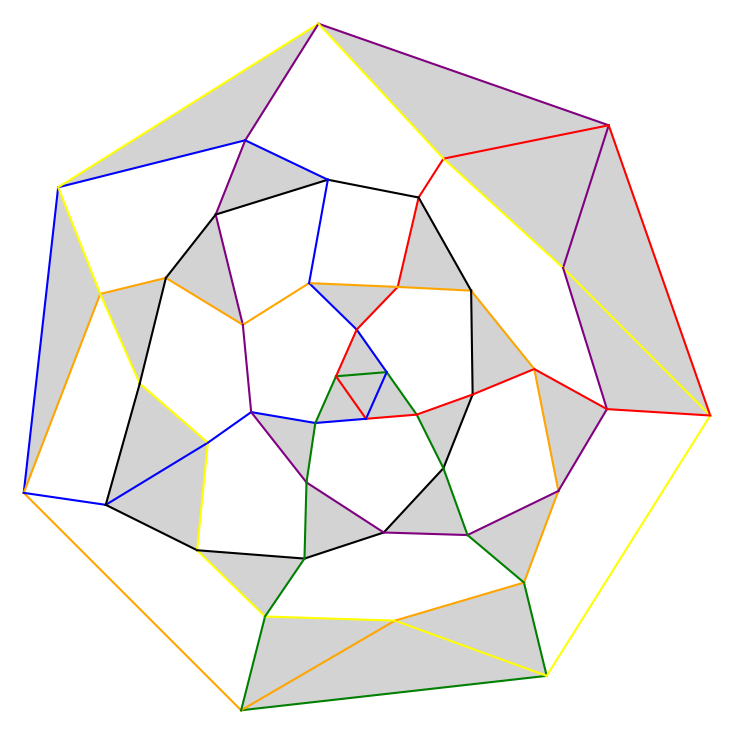
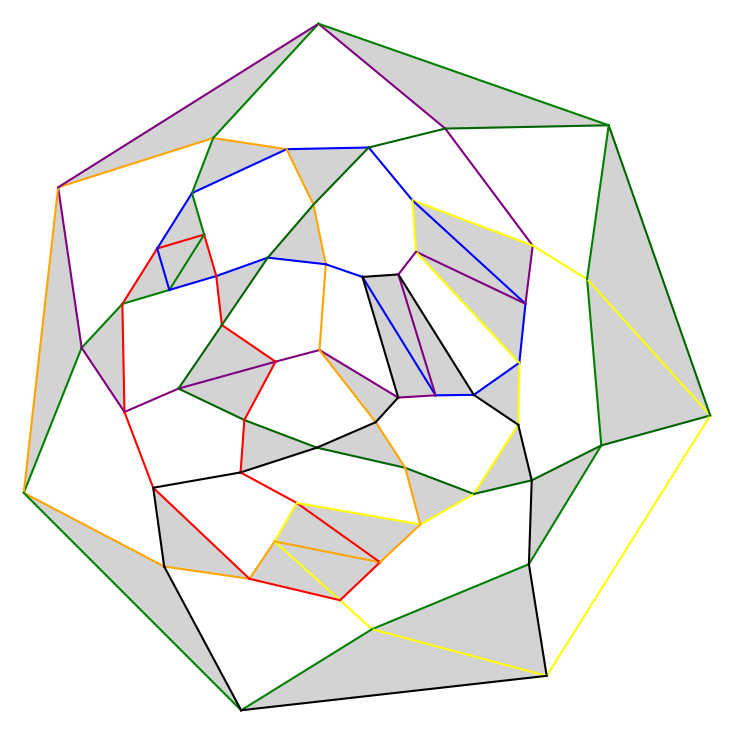
- arrangements of up to $n=7$ pseudocircles which obtain the maximum number of triangles (and some examples for $n=8,9$ which might be optimal), and
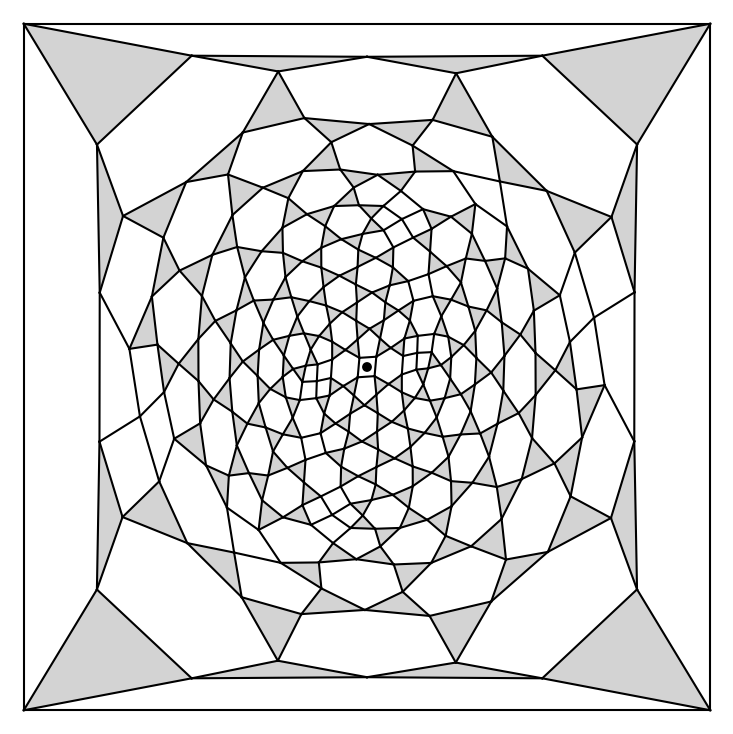
- small instances of an infinite family of arrangements which obtain an asymptotical triangle-cell-ratio of $2/3$.
Digonfree arrangement minimizing the number of triangles
File: triangles/digonfree_minimal_triangles/some13_df_18_triangles.txt (149.31 KB)
File: triangles/digonfree_minimal_triangles/some14_df_19_triangles.txt (7.63 KB)
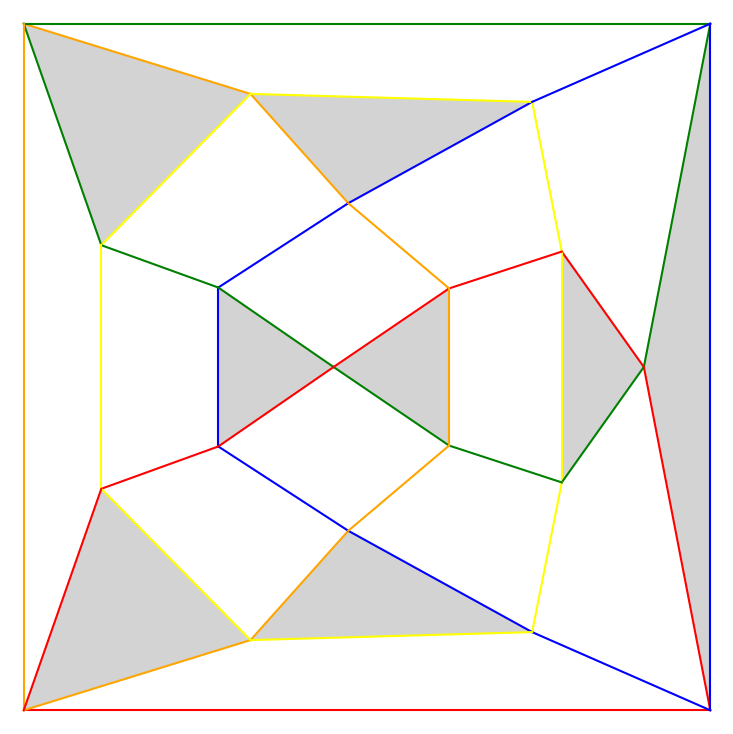
Digonfree arrangement maximizing the number of triangles
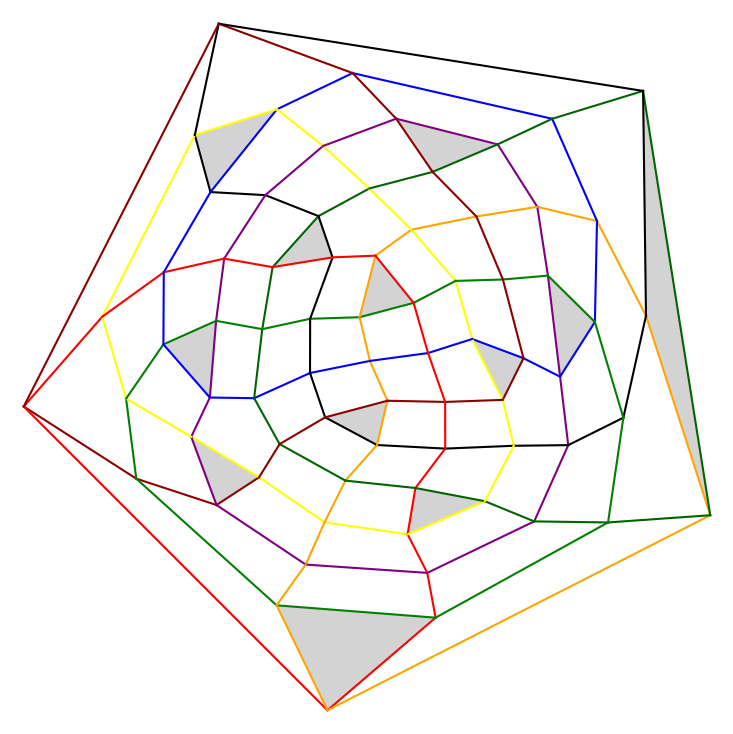
Fueredi Palasti Construction
This family of circularizable arrangements with $\lim_{n \to \infty} p_3/n^2 = 2/3$.File: triangles/fueredi_palasti_construction/fueredi_palasti_36.enc (5.11 KB)
File: triangles/fueredi_palasti_construction/fueredi_palasti_42.enc (6.98 KB)
Go back...Last update: July 09 2022 12:31:27.
(c) 2017 Stefan Felsner and Manfred Scheucher