K-Contact Representations
On this website we provide some examples to illustrate
the algorithm from
Equiangular polygon contact representations
by
Stefan Felsner,
Hendrik
Schrezenmaier, and
Raphael Steiner.
The input to this algorithm is a maximal planar graph with K vertices on the
outer face (these graphs are also known as inner triangulations of a K-cycle).
The goal is to compute a contact representation where each inner vertex is
represented by a regular K-gon (or a homothet of another individually prescribed equiangular K-gon) and the vertices of the outer face correspond
to the sides of the circumscribed K-gon.
The implementation and the website, in particular the generated pictures, are
due to
Hendrik
Schrezenmaier
and Manfred Scheucher.
Below on this page you find static pictures of contact representations with
K-gons. By clicking on the respective images you get to a page where the
iterative computation is visualized. The slider (green bullet) on the top of
these pages allows to move through the stages of the computation. When the
slider is on the right you see the contact representation. The continuous
motion is obtained by linear interpolation between consecutive stages
in the computation.
Have fun!
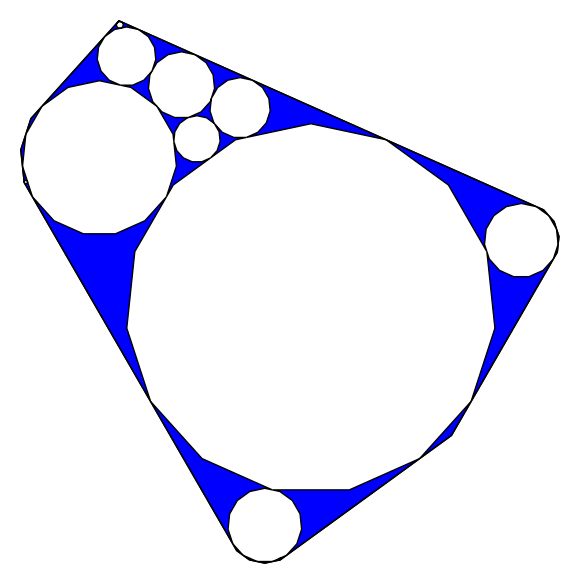
Some examples with regular polygons
K=3






K=5



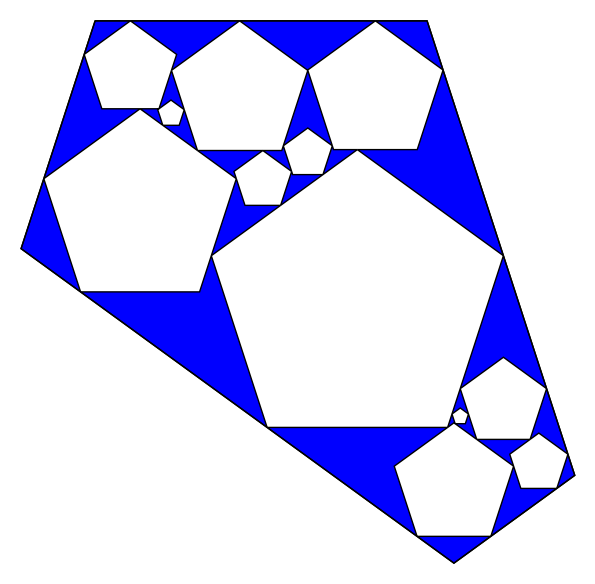
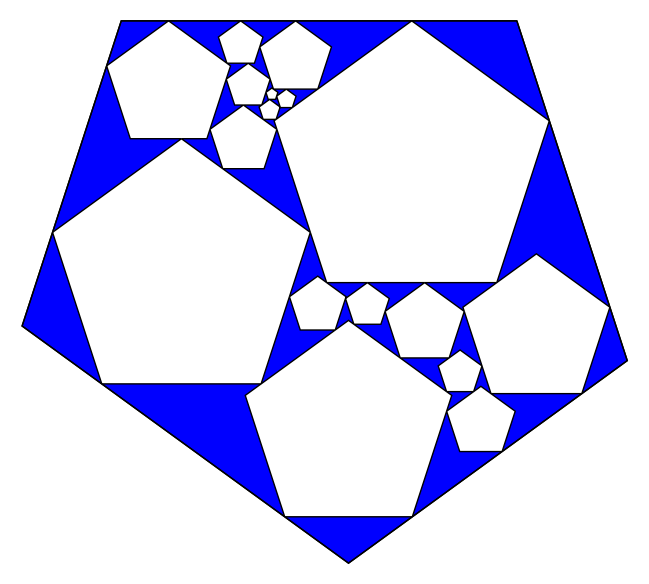

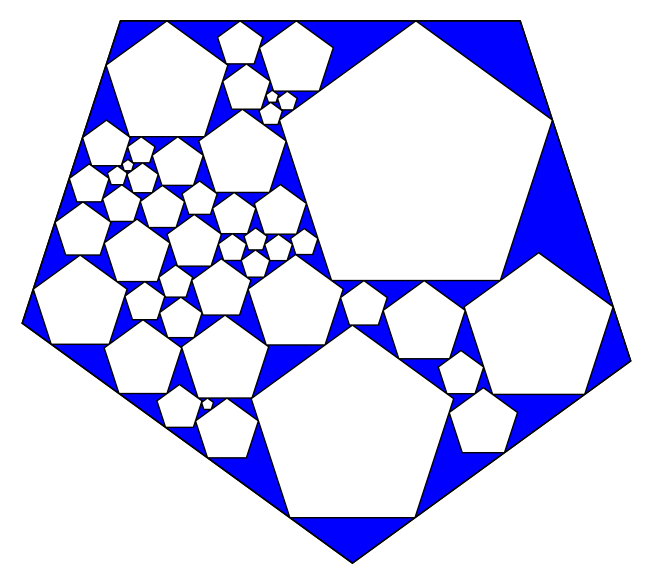
K=7
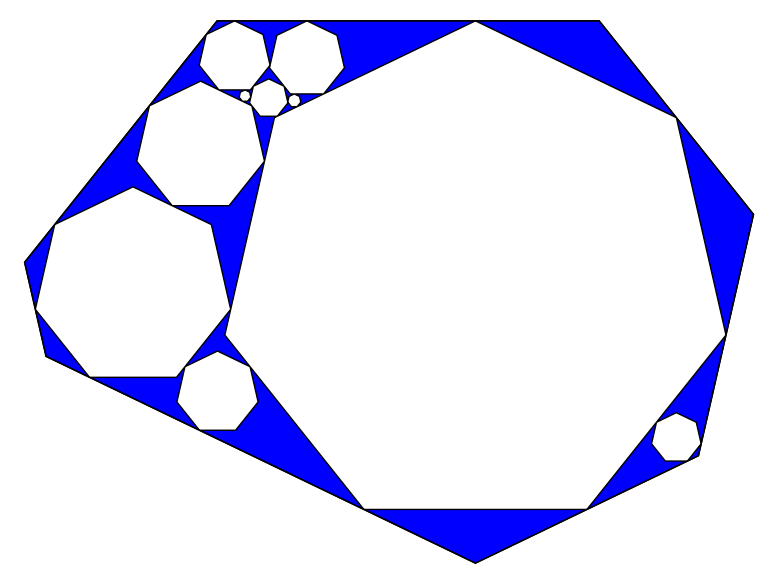
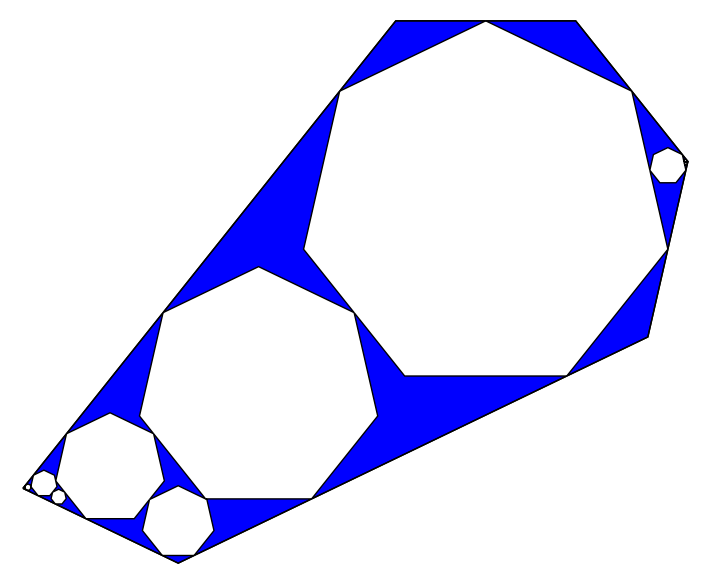
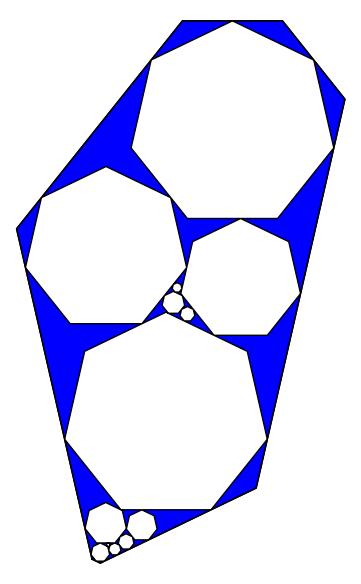


K=11


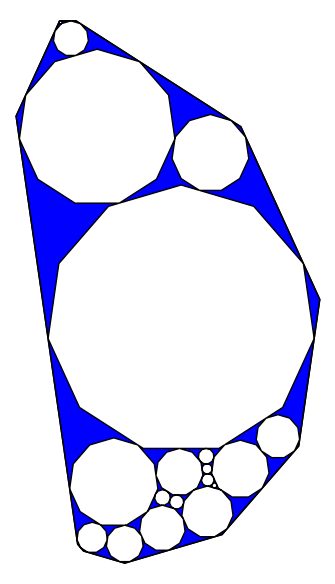
K=15
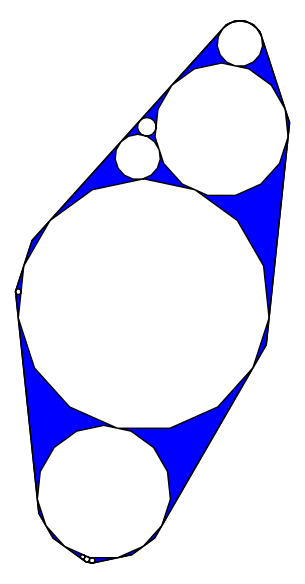
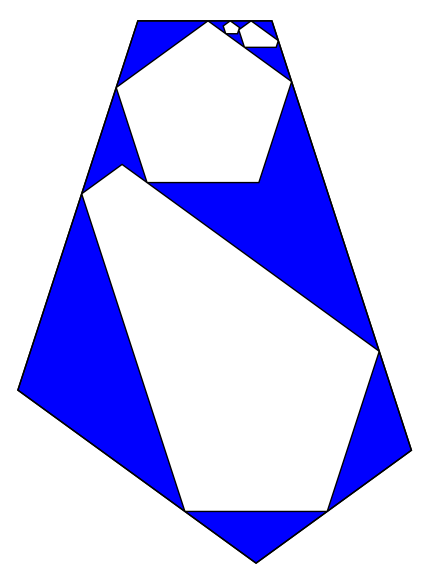
Some examples with irregular polygons
K=5

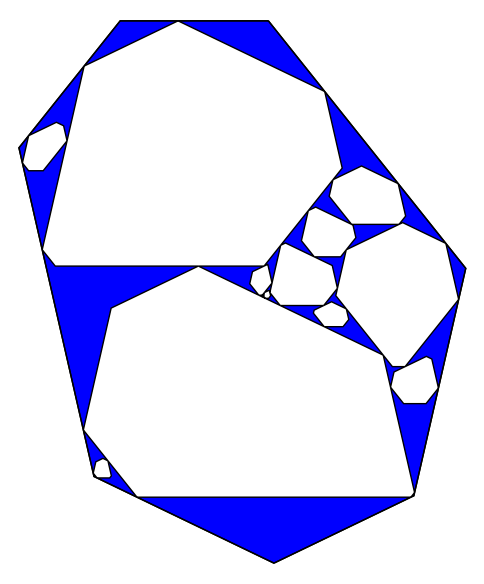
K=7
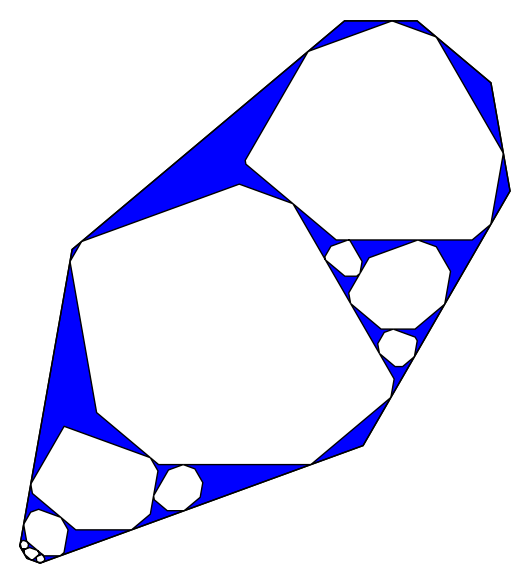
K=9
The number of iterations
The following graph classes show that, for each K, the number of iterations is at least linear in the worst case.



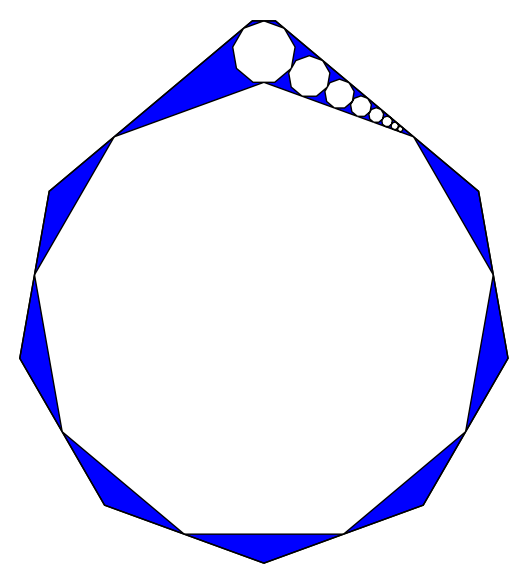
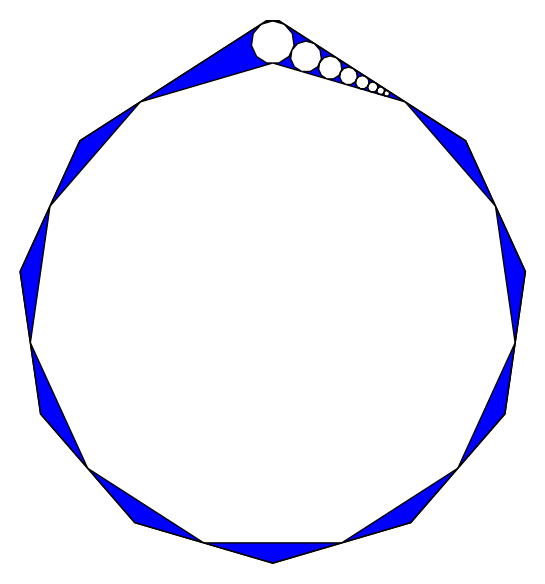
Maximal (known) numbers of iterations:
K=3, n=5: 2 iterations


K=3, n=6: 3 iterations
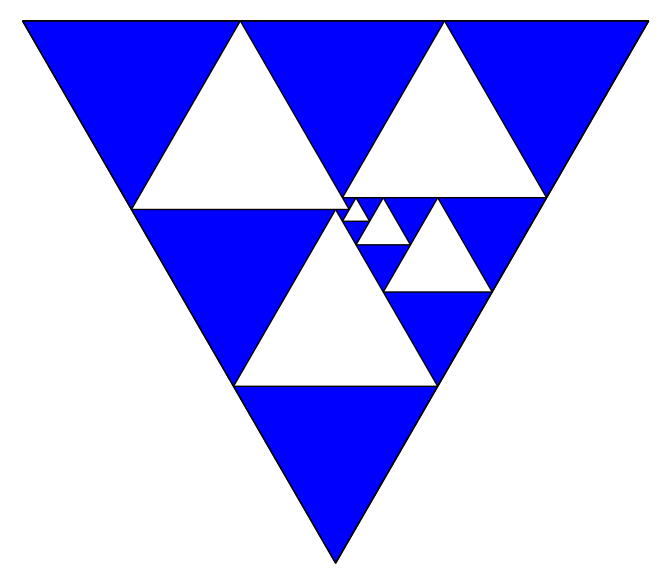
K=3, n=7: 4 iterations
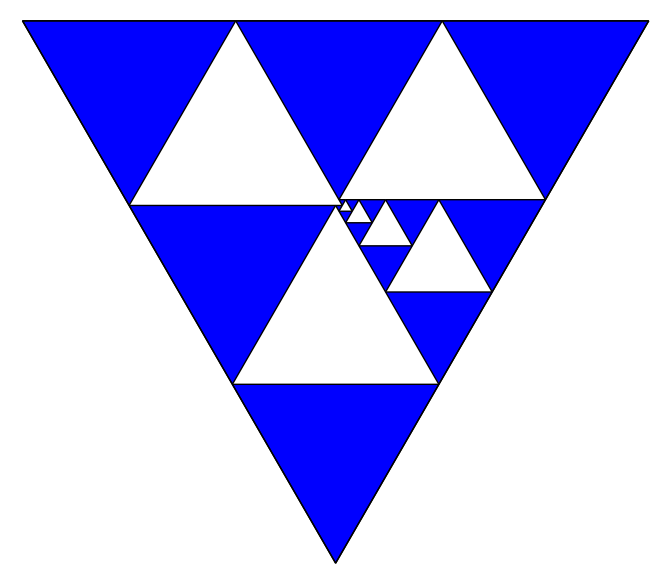
K=3, n=8: 5 iterations

K=5, n=4: 5 iterations
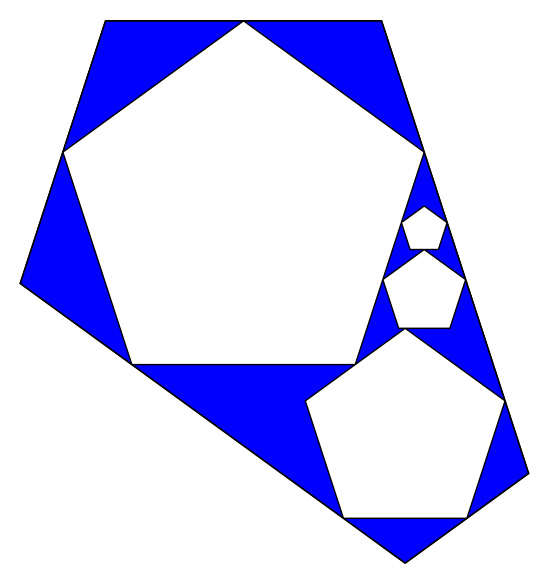
K=5, n=5: 6 iterations
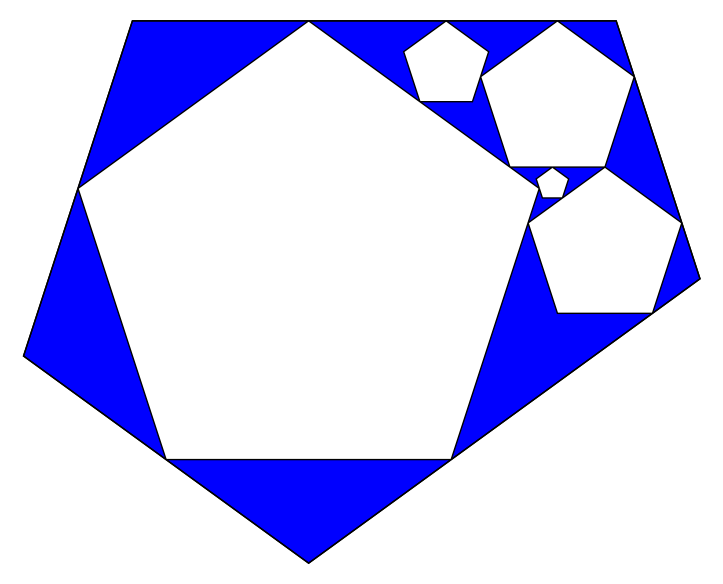



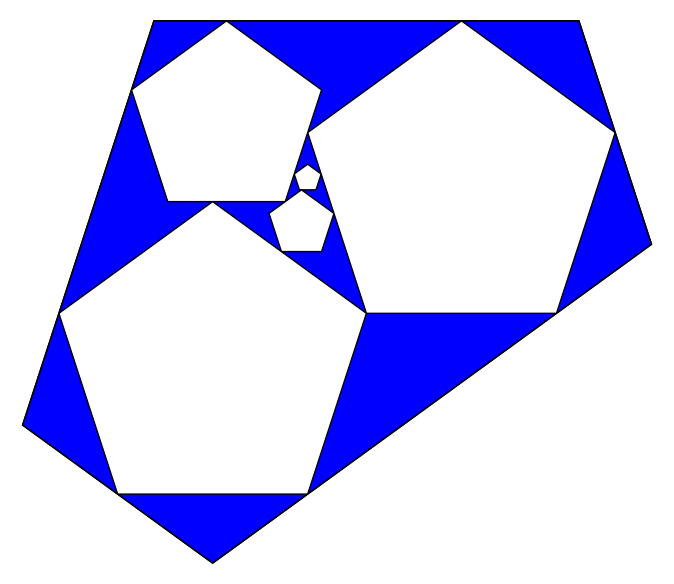
K=5, n=6: 8 iterations
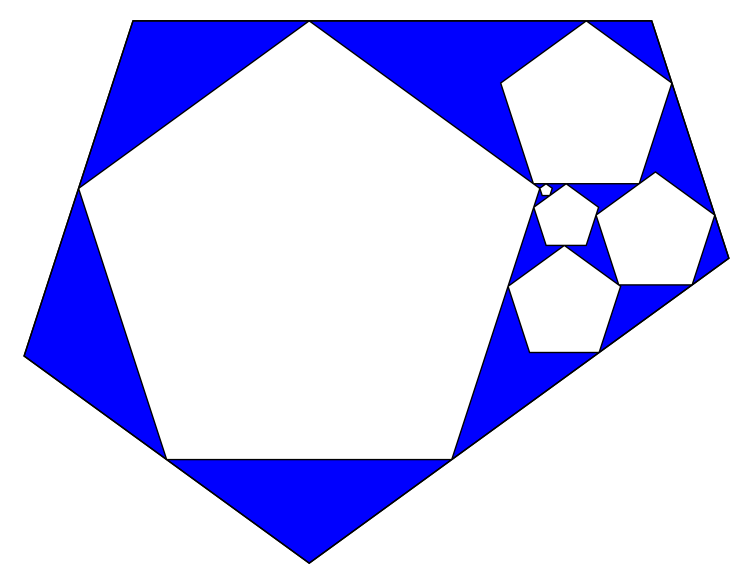
K=5, n=7: 9 iterations

K=5, n=8: 10 iterations














































