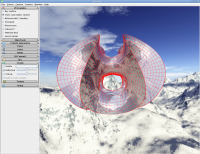
This screenshot shows the Chen-Gackstatter surface in the jReality VR viewer. This viewer allows loading 3D arbitrary data files but also includes a set of examples, several interesting mathematical surfaces as well as the Matheon baer, The whole GUI for this application is immersed into the 3D scene, so this application is also fully usable in immersive 3D environments (CAVEs). It includes easy alignment of the object and control of the appearance – how to render points, lines and faces of the displayed geometry.
To get started, simply look at the help tab.
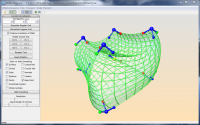
In this lab you may investigate surfaces of constant negative Gaussian curvature. Just drag the yellow points of the initial curve. For more information see the wiki page Discrete K_Surfaces.
In 2006 the International Mathematical Union (IMU) sponsored a contest to choose a new logo. The winning entry was from John Sullivan. This 4-minute animation introduces the mathematical significance of the logo and was shown at its unveiling in Madrid in 2006.
Animation was created using jReality's Renderman backend, rendered with Pixar's Photorealistic Renderman.
For more details see the credit frame of the video and Charles Gunn's project page.
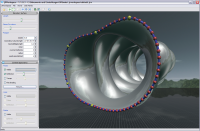
In this lab you may explore a version of Boy's surface that minimizes Willmore energy. Double click on the surface opens a panel which allows to adjust some exploration parameters. In particular you may start an animation, which draws the surface stretching a M?bius band until only one small disc is missing. This surface is the M?bius inversion of a minimal sphere with three planar ends. Adjusting the parameters called “Add in x,y,z” under “Appearance” you may alter the center of this M?bius inversion.
This lab was implemented by Elisabeth Guenther during the practice sessions of the course “Mathematische Experimente in Virtual Reality” winter 2006/07 using the jReality java package.
Three animations of a fluid jet modeled with discrete vortex fialemts: 1. Filaments, 2. Smoke particles, 3. Smoke around a sphere.
The animations were created by screen captures from the jogl-backend. Particle advection is performed on the graphics hardware (GPGPU). See A new doubly discrete analogue of smoke ring flow and the real time simulation of fluid flow. J. Phys. A: Math. Theor. 40 (2007), 12563-12576 or the preprint arXiv:0708.0979
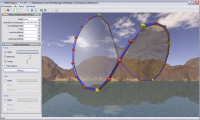
This lab solves the Plateau Problem interactively, i.e., finds the minimal surfaces with a given boundary. Double click on the surface opens the exploration panel, in which you may manipulate the parameters of the boundary curve. The yellow points on the boundary are draggable.
This lab was implemented by Simon Weiss during the practice sessions of the course “Mathematische Experimente in Virtual Reality” winter 2006/07 using the jReality java package.
This ViewerVR application demonstrates motion of water in a pool, modeled as shallow water waves.
This was created by Mohan Liu, as a student project for Mathematical Visualization WS 2008 ,
This ViewerVR application demonstrates a method for simulating fluid dynamics using a particle model.
This was created by Ivan Taranin, as a student project for Mathematical Visualization WS 2008 ,
This ViewerVR application provides two alternative methods to simulate the behavior of stretched membrane surfaces.
This application was created by Marius Schwalbe, as a student project for the course Mathematical Visualization WS 2008 .
The jreality VR plug-ins for the jRWorkspace. You can use the Minimal Surface Gallery or the 3D Xplore Math plug-ins as content generators.
This webstart is Java 1.6 only!
This webstart allows to explore 2D and 3D cyclidic nets in R3.
Cyclidic Discretization was implemented by Emanuel Huhnen-Venedey for his Diploma thesis “Curvature line parametrized surfaces and orthogonal coordinate systems. Discretization with Dupin cyclides”
See his web-page for details.
In this lab you may explore some minimal surfaces. It is an interactive version of some of Matthias Weber's Mathematica notebooks, see Matthias Weber's minimal surface museum.
This lab was implemented by Martin Beckmann during an intenship using the jReality java package.
A jReality application realizing different interactive visualizations in geometric knot theory.
Most program options are available via the context menu of corresponding components and their toolbars and sliders. For further information see the application's Help menu.
Diplomarbeit of Martin Sommer.
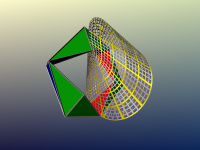
For each combinatorial type of convex 3-dimensional polyhedra, there exists a unique representative with the following properties:
- All edges are tangent to the unit sphere.
- The barycenter of the points where the edges touch the sphere is the origin.
This application (by Stefan Sechelmann) constructs this Koebe polyhedron for a given 3-connected planar graph.
Play with the fascinating motion of the so-called Schatz cube, a 6-hinge linkage with one degree of freedom. Observe how the motion generates the ruled surface called the oloid, and how a second oloid symmetric to the first rolls constantly along the first.
Explore 3-dimensional spaces, euclidean and non-euclidean. Featuring genuine real-time non-euclidean shading and innovative tools.
Yet another implementation of the Lorenz attractor, this time using jReality. A tutorial example created for the class Mathematical Visualization at TU Berlin.
A simple introduction to discrete groups and non-euclidean geometry, by means of reflections in the sides of a triangle. A tutorial example created for the class Mathematical Visualization at TU Berlin.
In this demo you can explore the stereographic projection of the sphere onto the plane. A tutorial example developed for the class Geometry I at TU-Berlin.