Research project C22

Adaptive solution of parametric eigenvalue problems for partial differential equations

Duration:

 August 2007 - May 2014

Project leaders:

 C. Carstensen, V. Mehrmann
Department of Mathematics, Humboldt-University of Berlin,
Unter den Linden 6, 10099 Berlin, Germany
Tel: +49 (0)30 - 209 35 489 (office) / - 209 35 844 (secretary)
email: cc@math.hu-berlin.de

Department of Mathematics, Technical University of Berlin,
Strasse des 17. Juni 136, 10623 Berlin, Germany
Tel: +49 (0)30 - 314 25 736 (office) / - 314 21 264
email: mehrmann@math.tu-berlin.de

Responsible:

 M. Schedensack, D. Gallistl
Department of Mathematics, Humboldt-University of Berlin,
Unter den Linden 6, 10099 Berlin, Germany
Tel: +49 (0)30 - 209 32 360
email: schedens@math.hu-berlin.de

Department of Mathematics, Humboldt-University of Berlin,
Unter den Linden 6, 10099 Berlin, Germany
Tel: +49 (0)30 - 209 32 360
email: gallistl@math.hu-berlin.de

Associated members:

 J. Gedicke, A. Międlar
Department of Mathematics, Humboldt-University of Berlin,
Unter den Linden 6, 10099 Berlin, Germany
Tel: +49 (0)30 - 209 32 360
email: gedicke@mathematik.hu-berlin.de

Department of Mathematics, Technical University of Berlin,
Strasse des 17. Juni 136, 10623 Berlin, Germany
Tel: +49 (0)30 - 314 21 263
email: miedlar@math.tu-berlin.de

Cooperation:

 There are connections to C29, C33, D23, D26

Support:

 DFG Research Center Matheon "Mathematics for Key Technologies"
Berlin Mathematical School

MATHEON project website:

Project C22


Guests

back to top

Background

Parameter dependent eigenvalue problems for partial differential equations (PDEs) arise in a large number of current technological applications. To mention only one example, parameter dependent eigenvalue problems arise in the computation of the acoustic field inside vehicles, such as cars or trains, or in analyzing the noise compensation in highly efficient motors and turbines.

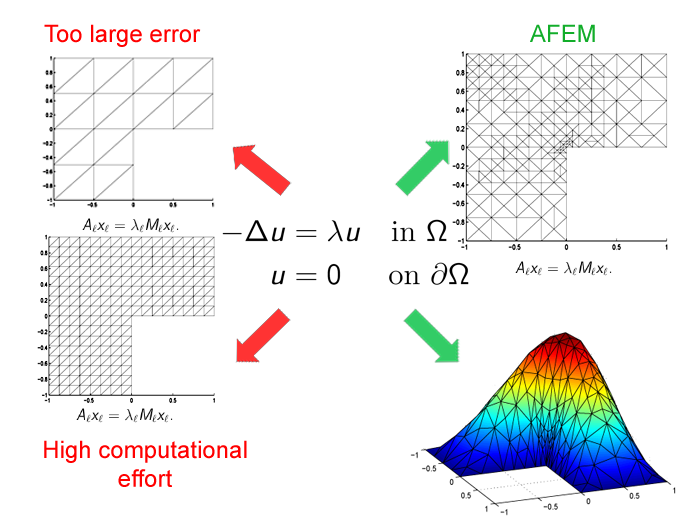
It is well understood that numerical methods for PDEs, such as finite element methods (FEM) with very fine meshes give good approximation but lead to a very high computational effort. Therefore it is important to use adaptively refined meshes to reduce the computational complexity while retaining good accuracy. This can be done by the adaptive finite element method (AFEM). But to do so, reliable and efficient error estimators especially for parameter dependent eigenvalue problem are needed. Since the general algebraic eigenvalue problem requires a lot of computational effort, especially for large sparse nonsymmetric systems, it is also an important task to develop fast iterative and multilevel eigenvalue solvers.

In combining these two research fields together, the goal is to equilibrate the errors and computational work between the discretization and the approximation errors and the errors in the solution of the resulting finite dimensional linear and nonlinear eigenvalue problems.

back to top

Highlights

A posteriori error estimators for the adaptive finite element method (AFEM) for elliptic symmetric eigenvalue problems have been improved. Global convergence for the refined edge residual-based error estimator has been shown without the usual assumption that the mesh-size is small enough.

Two combined adaptive algorithms for the finite element method and the linear algebraic eigenvalue problem have been developed and proven to be convergent. One of these has been shown to be of optimal computational complexity.

A full adaptive homotopy algorithm has been developed that adapts in all directions, the homotopy error, the finite element error and the algebraic error.

Some new functional perturbation results, i.e., functional backward error and functional condition numbers were introduced and used to establish a combined a posteriori error estimator embodying the discretization and the approximation error.

back to top

Publications

Journals

Proceedings

Submitted articles

Books

Theses

back to top

Talks

back to top

Posters

back to top
last updated: 2012-02-27